Формула Гауса-Остроградського
Іноді її називають формулою Остроградського-Гауса, іноді просто формулою
Остроградського. Потік векторного поля через замкнену поверхню
у напрямку зовнішньої одиничної
нормалі
дорівнює дивергенції даного
поля, обчисленої по тілу
, яке ця поверхня
обмежує:
Слід зазначити, що в оригіналі формула наводиться в зворотному порядку, і
її короткий зміст такий: інтеграл 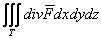 об'єднує дивергенцію по всьому
тілу, і якщо всередині нього є ТІЛЬКИ джерела або ТІЛЬКИ стоки, то відбувається
їх підсумовування. Якщо ж всередині є і те, і інше, то інтеграл «взаємовинищує»
елементарні потоки (дивергенції) різних знаків. Таким чином, у всіх випадках у
«сухому залишку» виходить потік через зовнішню поверхню.
об'єднує дивергенцію по всьому
тілу, і якщо всередині нього є ТІЛЬКИ джерела або ТІЛЬКИ стоки, то відбувається
їх підсумовування. Якщо ж всередині є і те, і інше, то інтеграл «взаємовинищує»
елементарні потоки (дивергенції) різних знаків. Таким чином, у всіх випадках у
«сухому залишку» виходить потік через зовнішню поверхню.
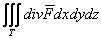 об'єднує дивергенцію по всьому
тілу, і якщо всередині нього є ТІЛЬКИ джерела або ТІЛЬКИ стоки, то відбувається
їх підсумовування. Якщо ж всередині є і те, і інше, то інтеграл «взаємовинищує»
елементарні потоки (дивергенції) різних знаків. Таким чином, у всіх випадках у
«сухому залишку» виходить потік через зовнішню поверхню.
об'єднує дивергенцію по всьому
тілу, і якщо всередині нього є ТІЛЬКИ джерела або ТІЛЬКИ стоки, то відбувається
їх підсумовування. Якщо ж всередині є і те, і інше, то інтеграл «взаємовинищує»
елементарні потоки (дивергенції) різних знаків. Таким чином, у всіх випадках у
«сухому залишку» виходить потік через зовнішню поверхню.
Однак формула частіше використовується так, як вона записана вище – щоб
трудомістке дослідження поверхні замінити обчисленням банального потрійного
інтеграла. Зокрема, якщо функція
являє собою ненульову константу,
то вся справа, по суті, зводиться до обчислення об'єму тіла.
Комментарии
Отправить комментарий